NumPyは、Pythonで数値計算を行うためのライブラリです。
行列や三角関数、平方根の計算等を最適化するように設計されていて、大規模な計算を高速に行うことができます。
NumPyの公式サイトはこちら
Contents
NumPyの準備
NumPyをインストール
では、早速インストールして使ってみましょう。
$ pip install numpyインストールできたか確認します。
$ pip list
Package Version
--------------- -------
〜(略)〜
numpy 1.20.2NumPyをインポート
Pythonから使用する場合は以下のようにインポートして使います。
npとして呼び出せるようにしていますが、慣例的にそうするみたいですね。
import numpy as np行列計算
行列・ベクトルの作成
NumPyでは、行列やベクトルをndarray型の配列(以下NumPy配列と呼びます)として取り扱います。
ベクトル(1次元配列)、行列のNumPy配列は、np.arrayメソッドに引数としてリストを渡すことで作成することができます。
行列では、引数に渡したリスト1つ1つが行列の行に相当します。
各行のリストは、さらにリストでラップするのを忘れないように注意です。
import numpy as np
# ベクトル(1次元配列)
a = np.array([1,2,3])
print(a) # [1 2 3]
print(a.shape) # (3,)
# 2×3行列
b = np.array([[1,2,3], [4,5,6]])
print(b)
# [[1 2 3]
# [4 5 6]]
print(a.shape) # (2, 3)ベクトル(1次元配列)の形状が(3,)になっているのは、要素数が1のタプルはカンマが付くという仕様によります。
NumPy配列の型は、<class 'numpy.ndarray'>のようにNumPyのndarray型として表現されます。
print(type(a)) # <class 'numpy.ndarray'>タプルからNumPy配列を作ることもできます。
c = np.array((1,2,3))
print(c) # [1 2 3]行列計算
一般的に、行列の積は以下のように計算します。
\[
\begin{bmatrix}
a_{11} & a_{12} & \dots & a_{1m} \\
a_{21} & a_{22} & \dots & a_{2m} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \dots & a_{nm} \\
\end{bmatrix}
\begin{bmatrix}
b_{11} & b_{12} & \dots & b_{1p} \\
b_{21} & b_{22} & \dots & b_{2p} \\
\vdots & \vdots & \ddots & \vdots \\
b_{m1} & b_{m2} & \dots & b_{mp} \\
\end{bmatrix}=
\begin{bmatrix}
c_{11} & c_{12} & \dots & c_{1p} \\
c_{21} & c_{22} & \dots & c_{2p} \\
\vdots & \vdots & \ddots & \vdots \\
c_{n1} & c_{n2} & \dots & c_{np} \\
\end{bmatrix}
\]
\[
c_{ij}=\sum_{k=0}^{m}a_{ik}b_{kj}
\]
NumPyで以下の計算をしてみましょう。
\[
A=\begin{bmatrix}
1 & 2 \\
3 & 4 \\
5 & 6 \\
\end{bmatrix}
\quad
B=\begin{bmatrix}
11 & 12 & 13 & 14 \\
15 & 16 & 17 & 18 \\
\end{bmatrix}
\]
\[
C=A\cdot B=\begin{bmatrix}
1\cdot11+2\cdot15 & 1\cdot12+2\cdot16 & 1\cdot13+2\cdot17 & 1\cdot14+2\cdot18 \\
3\cdot11+4\cdot15 & 3\cdot12+4\cdot16 & 3\cdot13+4\cdot17 & 3\cdot14+4\cdot18 \\
5\cdot11+6\cdot15 & 5\cdot12+6\cdot16 & 5\cdot13+6\cdot17 & 5\cdot14+6\cdot18 \\
\end{bmatrix}\\
=\begin{bmatrix}
41 & 44 & 47 & 50 \\
93 & 100 & 107 & 114 \\
145 & 156 & 167 & 178 \\
\end{bmatrix}
\]
行列の積はnp.dot(行列A, 行列B)メソッドで計算できます。
行列の積を計算する場合は、1つ目の行列の列数と2つ目の行列の行数を合わせる必要があります。
上の計算の例で言うと、aの列数(2)、bの行数(2)が一致していますね。
import numpy as np
a = np.array([[1,2], [3,4], [5,6]])
print(a.shape) # (3, 2)
b = np.array([[11,12,13,14], [15,16,17,18]])
print(b.shape) # (2, 4)
# aの列数(2)とbの行数(2)が一致している!
c = np.dot(a, b)
print(c)
# [[ 41 44 47 50]
# [ 93 100 107 114]
# [145 156 167 178]]
print(c.shape) # (3, 4)ベクトル(1次元配列)同士の積は内積の計算になり、スカラー値として返ってきます。
import numpy as np
a = np.array([1,2,3]) # (3,)
b = np.array([4,5,6]) # (3,)
c = np.dot(a, b)
print(c) # 32
print(type(c)) # <class 'numpy.int64'>要素が0,1の行列
np.zeros(),np.ones()で要素が0または1のNumPy配列を作成できます。
import numpy as np
z = np.zeros(3)
o = np.ones(3)
print(z) # [0. 0. 0.]
print(o) # [1. 1. 1.]2次元以上の配列は、次元数をタプルで渡してあげます。
z = np.zeros((3,4))
o = np.ones((3,4))
print(z)
# [[0. 0. 0. 0.]
# [0. 0. 0. 0.]
# [0. 0. 0. 0.]]
print(o)
# [[1. 1. 1. 1.]
# [1. 1. 1. 1.]
# [1. 1. 1. 1.]]ブロードキャスト
ブロードキャストは、行列の計算時にNumPy配列の形状を合わせることができる機能です。
例えば、以下のような計算をしたいとします。
\[
2\cdot\begin{bmatrix}
1 & 2 \\
3 & 4 \\
\end{bmatrix}
\]
行列の各要素にそれぞれ2を掛けて答えは
\[
\begin{bmatrix}
1\cdot2 & 2\cdot2 \\
3\cdot2 & 4\cdot2 \\
\end{bmatrix}=\begin{bmatrix}
2 & 4 \\
6 & 8 \\
\end{bmatrix}
\]
になりますね。
このように、私たちは行列の各要素に2を掛けるという操作を無意識的に行なっています。
しかしPythonでは行列の要素数を合わせてあげないと計算させることができません。
そこで、計算対象のNumPy配列の型を自動的に合わせてくれる機能がブロードキャストです。
以下の例では、ブロードキャスト機能を使って、整数の2をNumPy配列([[2 2] [2 2]])の型に自動で変換しています。
import numpy as np
A = np.array([[1,2], [3,4]])
# [[1 2]
# [3 4]]
c = 2
print(c * A)
# [[2 4]
# [6 8]]
# ブロードキャスト機能で整数の2をNumPy配列([[2 2] [2 2]])の型に自動で変換している。
# 2 * [[1 2] [3 4]] => [[2 2] [2 2]] * [[1 2] [3 4]]足し算についても、同様にブロードキャストしてくれます。
import numpy as np
A = np.array([[1,2], [3,4]])
# [[1 2]
# [3 4]]
c = 2
print(c + A)
# [[3 4]
# [5 6]]
# ブロードキャスト機能で整数の2をNumPy配列([[2 2] [2 2]])の型に自動で変換している。
# 2 + [[1 2] [3 4]] => [[2 2] [2 2]] + [[1 2] [3 4]] = [[2 3] [4 5]]演算機能
三角関数
以下のNumPy関数を使って、三角関数の演算ができます。
- np.sin() (正弦関数)
- np.cos() (余弦関数)
- np.tan() (正接関数)
引数はラジアンで渡してあげます。
import numpy as np
print(np.sin(1)) # sin(1) = 0.8414709848078965
print(np.cos(1)) # cos(1) = 0.5403023058681398
print(np.tan(1)) # tan(1) = 1.557407724654902np.piでπ(円周率)を使うこともできます。
import numpy as np
print(np.pi) # π = 3.141592653589793
print(np.cos(np.pi)) # cos(π) = -1.0逆三角関数も使えます。
- np.arcsin() (逆正弦関数)
- np.arccos() (逆余弦関数)
- np.arctan() (逆正接関数)
import numpy as np
print(np.arcsin(1)) # 1.5707963267948966
print(np.arccos(1)) # 0.0
print(np.arctan(1)) # 0.7853981633974483sin(x)をplotするとこんな感じです。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.01)
y = np.sin(x)
plt.plot(x, y)
plt.show()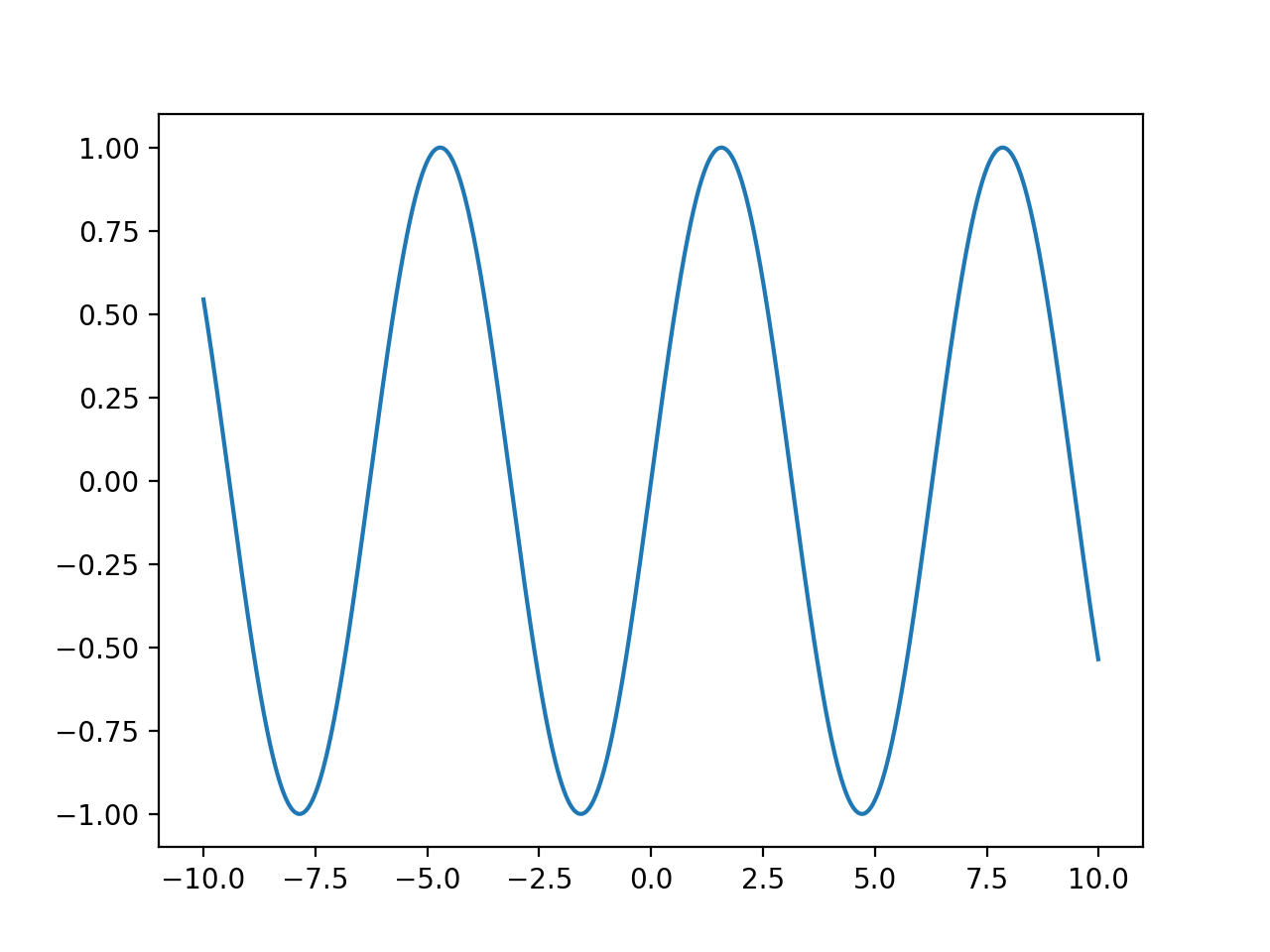
平方根・立方根・自乗
平方根・立方根・自乗をそれぞれ計算できます。
- np.sqrt() (平方根)
- np.cbrt() (立方根)
- np.square() (自乗)
import numpy as np
# 平方根
print(np.sqrt(4)) # 2.0
# 立方根
print(np.cbrt(27)) # 3.0
# 自乗
print(np.square(5)) # 25ネイピア数「e」
np.eでネイピア数自体を出力できます。
import numpy as np
print(np.e) # 2.718281828459045np.exp()でネイピア数「e」の階乗を扱えます。
import numpy as np
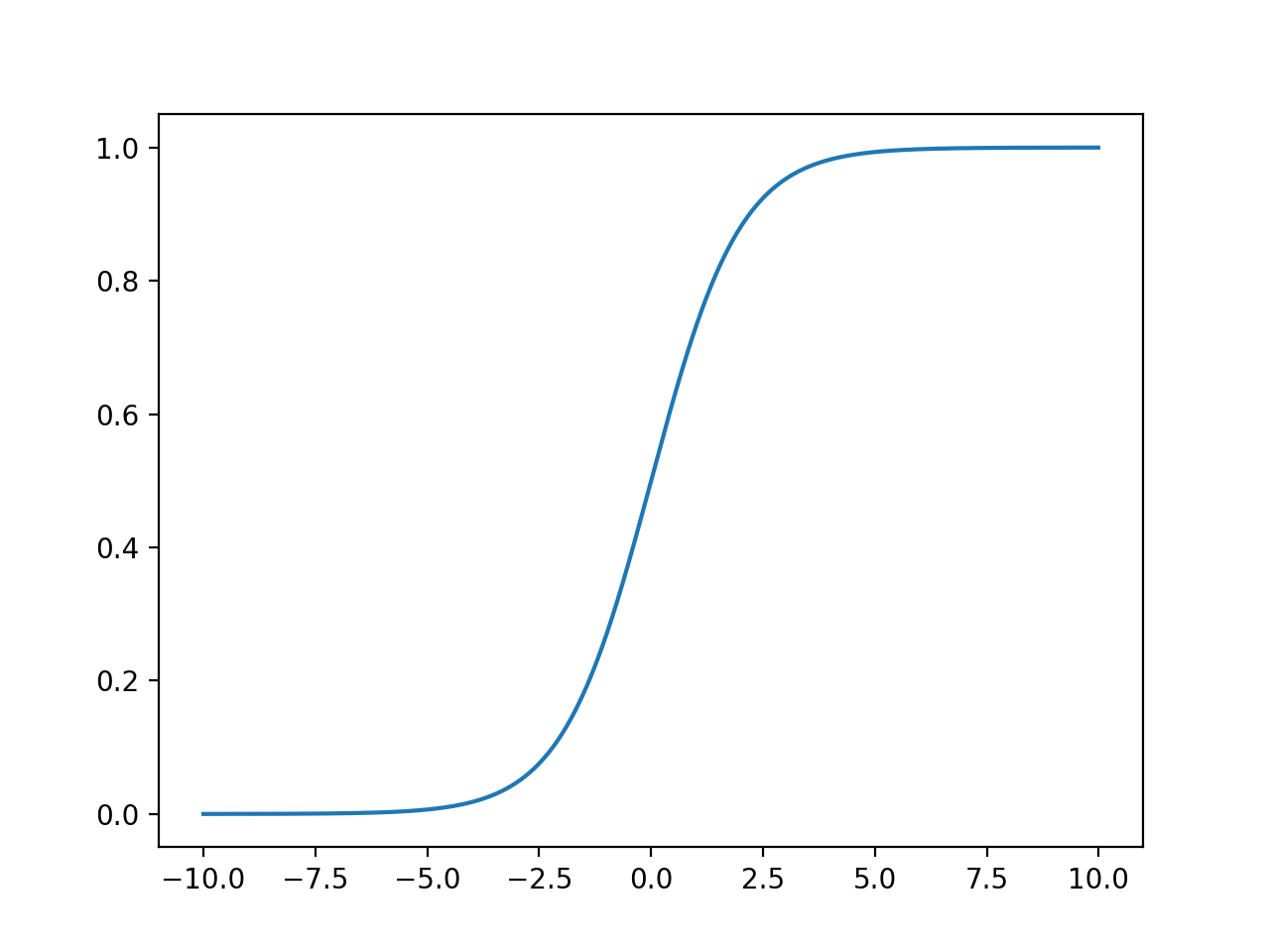
print(np.exp(2)) # e^2 = 7.38905609893065機械学習の活性化関数として知られるシグモイド関数は以下のようにプロットできます。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-10, 10, 0.01)
y = 1 / (1 + np.exp(-x)) # シグモイド関数
plt.plot(x, y)
plt.show()